Crack calculation

CSA S6

Code Approach

The equation for the crack width is given in section 8.12.3.2 as

$$w=k_b\beta_cs_{rm}\varepsilon_{sm}$$

The parameters $k_b$ and $\beta_c$ depend on the section and the cause of cracking. The code defines $s_{rm}$ in mm as

$$s_{rm}=50+0.25k_c \frac{d_b}{\rho_c}$$

Where

$$\rho_c=\frac{A_s}{A_{ct}}$$

and $A_{ct}$ is the concrete area excluding the reinforcement. The code gives values for $k_c$ as 0.5 for bending and 1.0 for pure tension. In AdSec we interpolate between these values using

$$k_c=\frac{(\varepsilon_{max}+max(\varepsilon_{min},0))}{2 \times max(|\varepsilon_{max}|,|\varepsilon_{min}|)}$$

But limited to the range [0.5:1].

The $d_b$ term is taken as the average bar diameter in the tension zone, and the area of steel in $\rho_c$ is taken as the weighted area of the bar in the tension zone

$$A_s=\Sigma \space a_i \frac{\pi \space d_i^2}{4}$$

And the weighting is based on the stress in the bar compared with the stress in the extreme bar.

$$a=\frac{\sigma_i}{\sigma_{extreme}}$$

The area of concrete in $\rho_c$ is

$$A_c=min(A_c(2.5h_t),A_c(h_b/3))$$

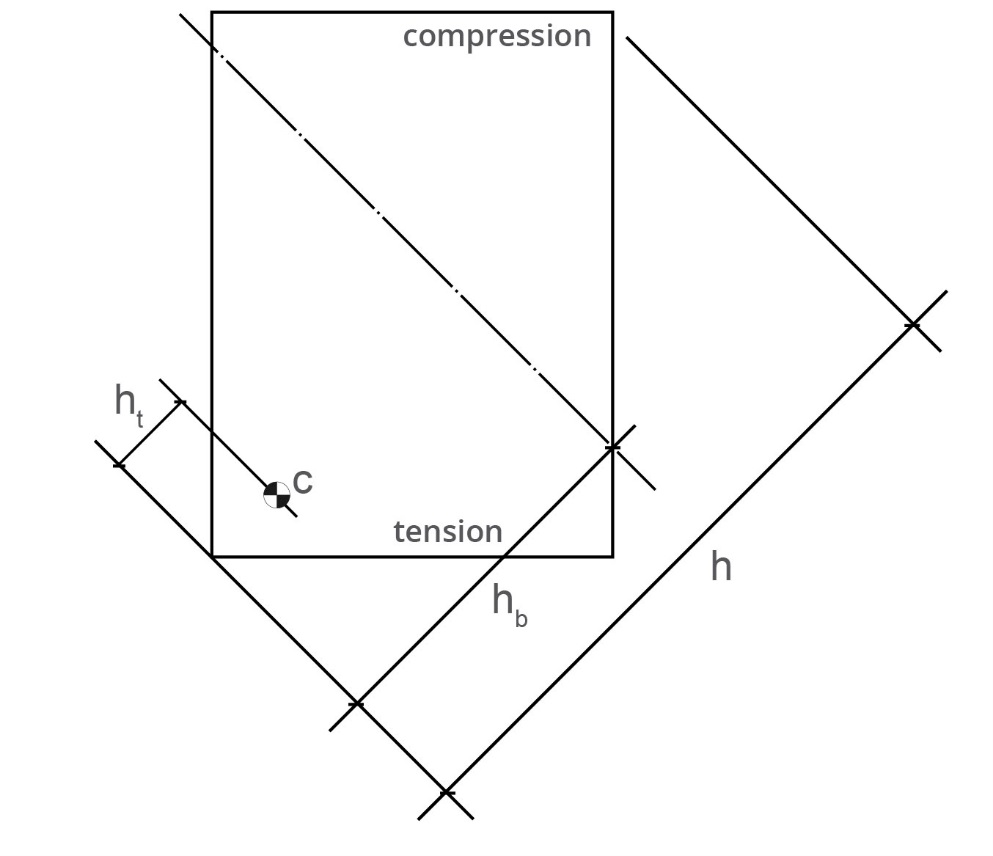
where c is the centroid of reinforcement in tension. The strain term is given in the code as

$$\varepsilon_{sm}=\frac{f_s}{E_s}\Bigr[1-\Bigl(\frac{f_w}{f_s}\Bigl)^2\Bigr]$$

Where $f_s$ is the stress in the reinforcement at the serviceability limit state and $f_w$ is the stress in the reinforcement at initial cracking. In AdSec this is implemented as

$$\varepsilon_{sm}=\frac{\sigma_s}{E_s}\Bigr[1-\Bigl(\frac{f_{c,rup}}{\sigma_{ct}}\Bigl)^2\Bigr]$$

Where $\sigma_s$ is the stress in the most tensile reinforcement at the serviceability for a fully cracked calculation, $f_{c,rup}$ is the rupture strength of the concrete and $\sigma_{ct}$ is the maximum tensile stress in the concrete at the extreme fibre assuming an uncracked material.

Local Approach

The above approach becomes difficult to justify when the section is not in uniaxial bending. In these cases the alternative local approach can be used. This assumes there is a local relationship between a bar and the surrounding concrete.

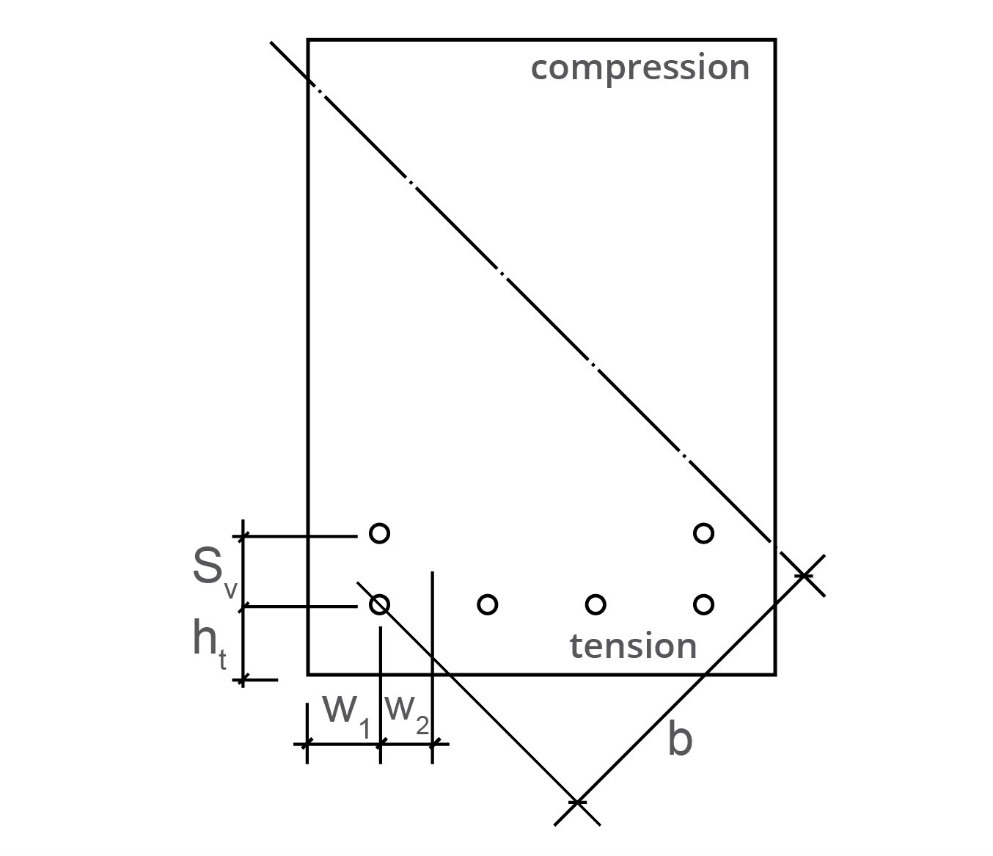
The first stage is to identify the most tensile bar and determine the cover $c$ to this bar. We then define $h_t$ as the cover plus half the bar diameter.

$$h_t=c+\frac{d_b}{2}$$

The depth from the neutral axis the most tensile bar $b$ is calculated, and $h_b$ is then defined as

$$h_b=b+c+\frac{d_b}{2}$$

Then the concrete area is based on a dimension

$$h_c=min(2.5h_t,h_b/3,(h_t+s_v/2))$$

The width associated with this is

$$w_c=min(5h_t,(w_1+w_2))$$

So that

$$A_c=h_c\times w_c$$

EN1992-1

The equation for the crack width is equation 7.8

$$w_k=s_{r,max}(\varepsilon_{sm}-\varepsilon_{cm})$$

In this $s_{r,max}$ is given by

$$s_{r,max}=k_3c+k_1k_2k_4\phi/\rho_{p,eff}$$

The code gives values for $k_1$ as 0.8 for high bond bars and 1.6 for plain bars or pre-stressing tendon. The code gives values for $k_2$ as 0.5 for bending and 1.0 for pure tension. In AdSec we interpolate between these values using

$$k_c=\frac{(\varepsilon_{max}+max(\varepsilon_{min},0))}{2\times max (|\varepsilon_{max}|,|\varepsilon_{min}|)}$$

But limited to the range [0.5:1]. $k_3$ and $k_4$ are nationally determined parameters which default to 3.4 and 0.425 respectively.

Where the spacing of bar is large, $>5(c+\phi/2)$, then

$$s_{r,max}=1.3(h-x)$$

$\rho_{p,eff}$ is the ratio of reinforcement to concrete in the cracking zone where the area of concrete is defined as

$$A_{c,eff}=min(A_c(2.5(h-d),A_c((h-x)/3),A_c(h/2)))$$