Elastic-hardening
The initial slope is defined by the elastic modulus, , after yield the hardening modulus governs as stress rises from () to (). For EN 1992 the hardening modulus is defined in terms of a hardening coefficient and the final point is () where the failure strain is reduced to (typically ).
The relationship between hardening modulus and hardening coefficient is:
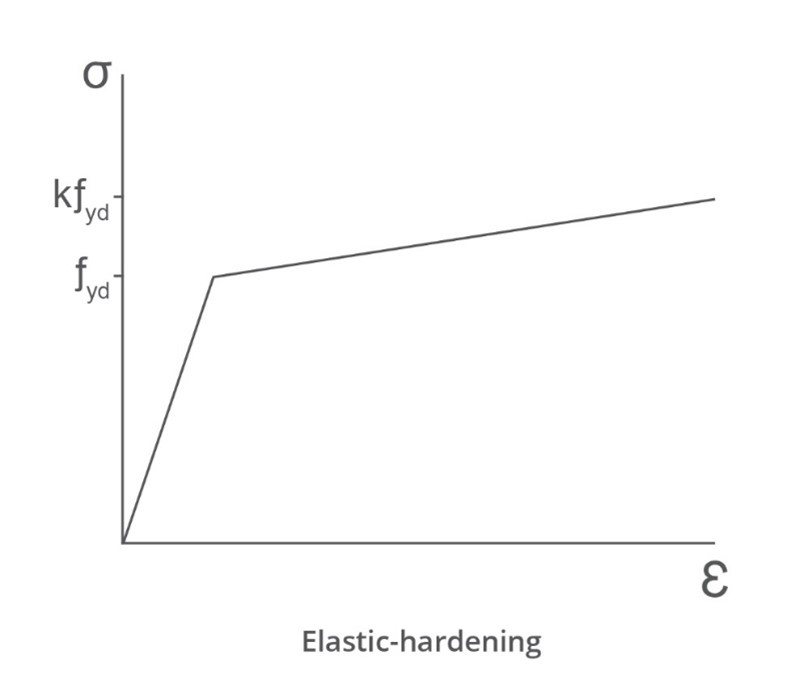
The material fails at where . This is defined in Eurocode and related codes.