Alternative stress blocks
General stress blocks
Parabola-rectangles are commonly uses for concrete stress-strain curves.
The parabolic curve can be characterised as
fcf=a(εpε)2+b(εpε) Define
f′=fcf and
η=εpε 
If the curve is taken to be tangent to the plateau then at n=1,f′=1 and dηdf′=0.
Solving for the coefficients gives a=−1 and b=2 so
f′=2η−η2 The area under the curve is given by
Ap=∫01f′dη=[η2−3η3]01=32 For bi-linear curve with the strain transition at εb the area under the curve to εp is
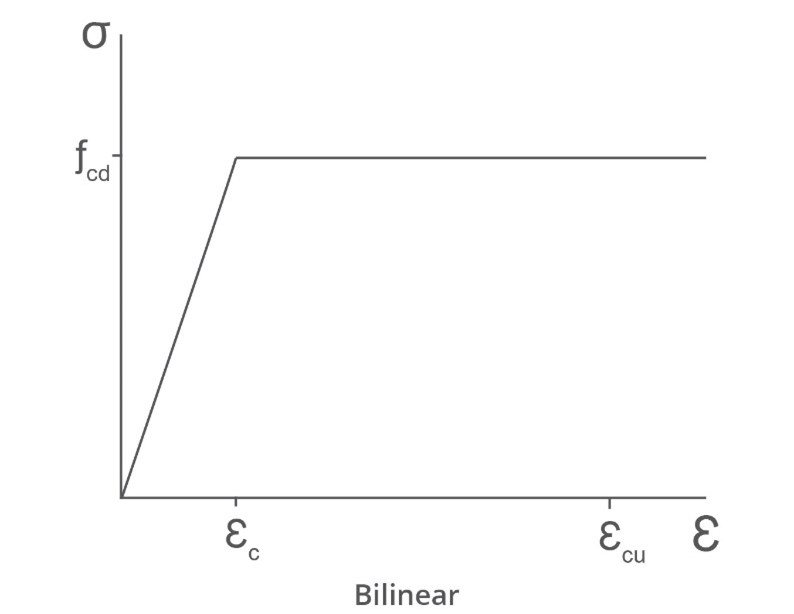
Ab=2ηb+(1−ηb)=1−2ηb Equating the areas
1−2ηb=32 or
ηb=32 So
εc,b=32εc,p For a rectangular stress block with the strain transition at εr the area under the curve to εp is
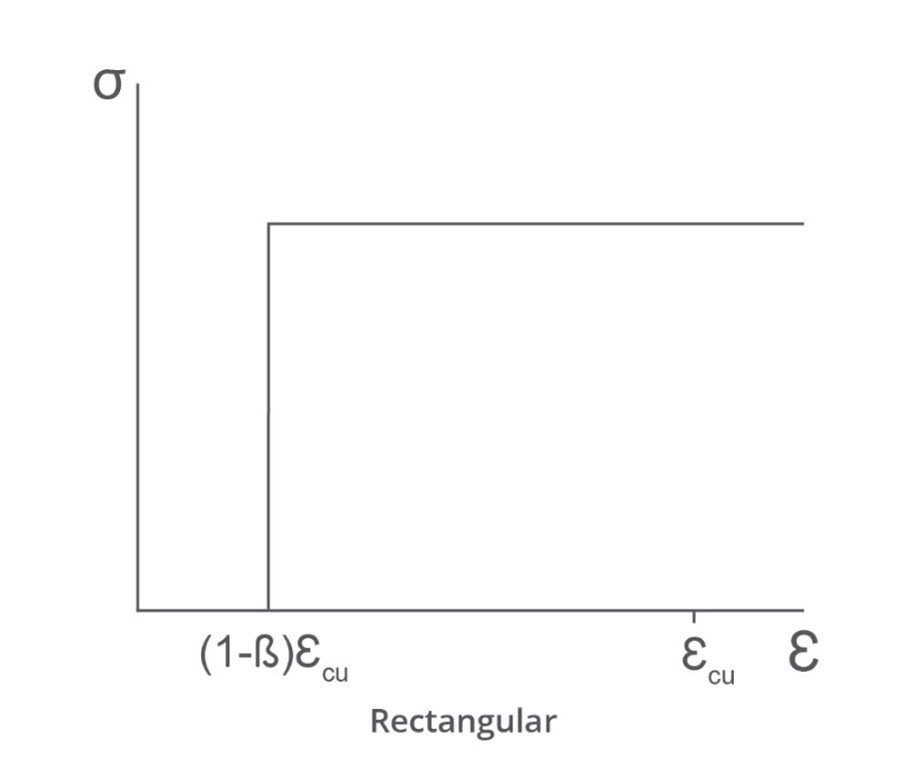
Ab=1−ηr Equating the areas
1−ηr=32 or
ηr=31 so
εcJ=31εc,p 

