Beam axes
Symmetry about the axis
In most cases beams have symmetry about one axis or both axes (e.g., a rectangular, circular, I-beam or tee section). In these cases the principal axes of the beam correspond with the local axes. This means that the bending behaviour is governed by: and and the term is zero.
No symmetry about the axis
When a section lacks symmetry about both axes, the cross term is no longer zero. This means that a load in the y direction will produce a displacement in y and z directions.
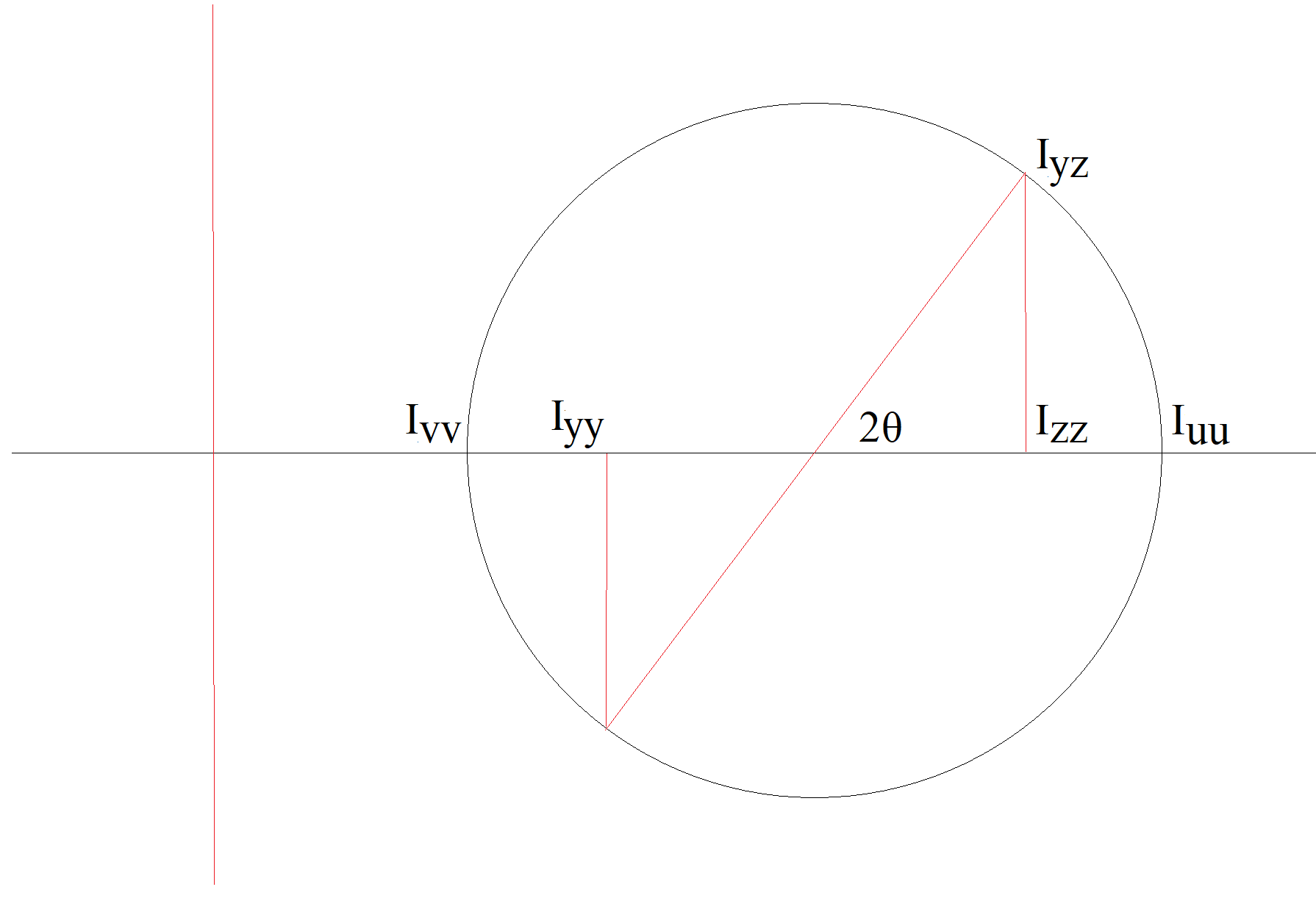
The angle of the principal second moments of area can be calculated from:
The second moments of area in the u and v axes are:
These relationships can be visualised using a Mohr's circle approach similar to stress.
Note: GSA gives the option to use either principal second moments of area, or local second moments of area (ignoring the term). Principal moments most often apply to asymmetric or angle sections; by using this option it is possible to capture sideways deflection. Therefore, the latter option is not recommended.