Axis Sets
Axes
In order to make the most of GSA it is important to understand the axis systems available in GSA and how they are used. The term axis is used to refer to axis sets or coordinate systems. The axis sets can be either Cartesian , cylindrical , or spherical . Spherical axis follow the physics (ISO) convention: radial distance , polar angle (theta), and azimuthal angle (phi).
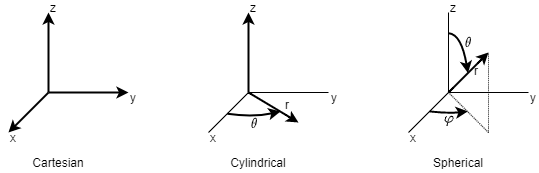
The basic axis system is the Global Cartesian axis system, normally referred to as the Global axis system. All other axis systems are located relative to the Global axis system. Global axis directions are generally denoted X, Y and Z to distinguish from other, more general axis directions which use x, y and z.
Note that for cylindrical axes, if the radius () is zero then the theta angle () is arbitrary and treated as zero. Similarly for spherical axes, if the radius () is zero then the theta () and phi () angles are treated as zero, and if the theta angle () is zero then the phi angle () is treated as zero.
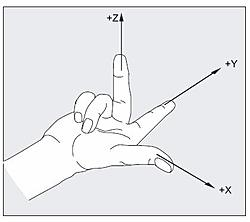
All the axes systems in GSA are right handed axes systems.
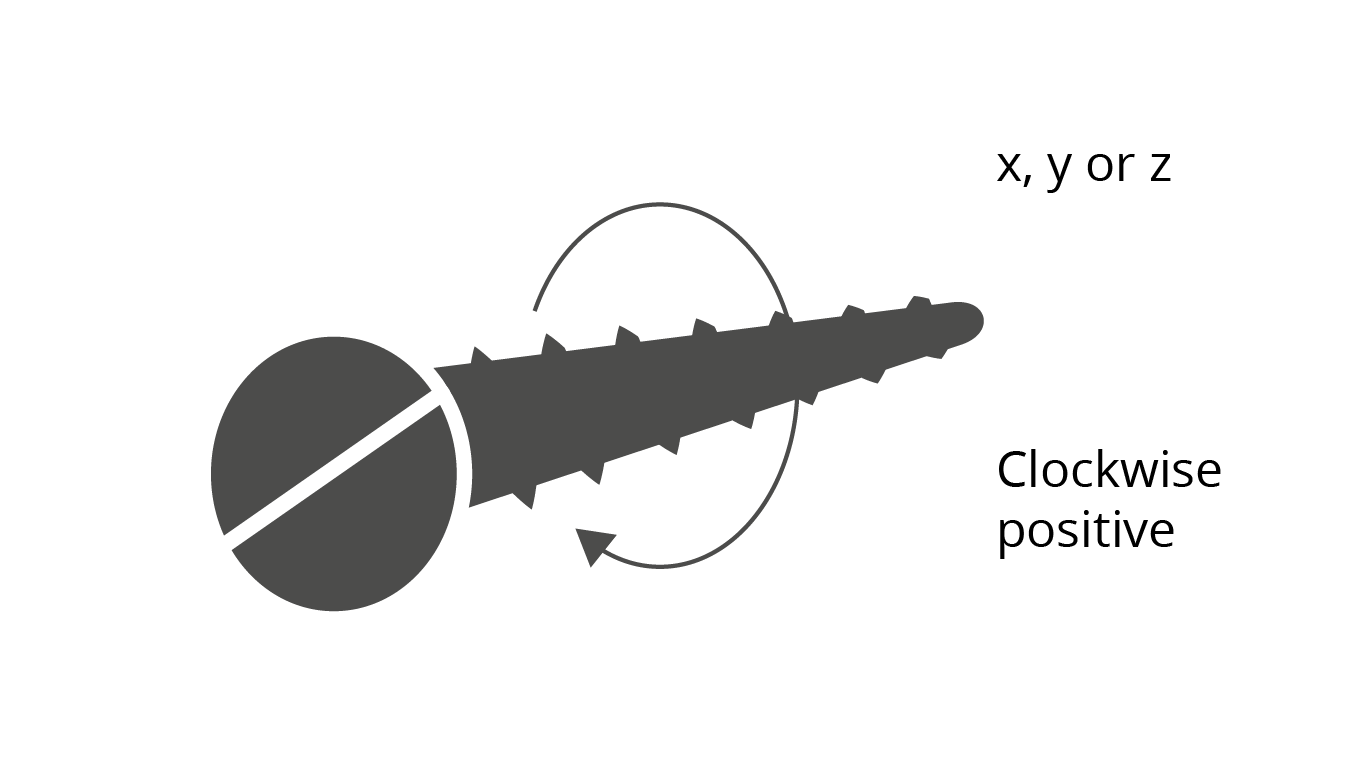
Rotations about the axes follow the right hand screw rule
Predefined Axes
There are a number of predefined axes systems:
- X elevation – to give an plane for the X elevation (origin at global origin, in -Y, in Z and in -X).
- Y elevation – to give an plane for the Y elevation (origin at global origin, in X, in Z and in -Y)
- Vertical – to give a vertically aligned axis set (origin at global origin, in Z, in X and in Y)
- Global cylindrical – origin at global origin, in Z and in X
User Defined Axes
In addition to these are user defined axes. User defined axes can be either Cartesian, cylindrical or spherical and are located in space by an origin. The axis is defined by a vector direction in the axis () direction and the plane () of the axis is defined by any vector lying in the plane. The axis set is then constructed from these vectors.