Skip to main content

Axes

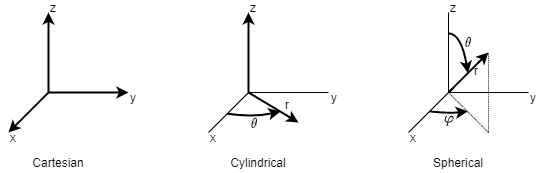
Axes can be either Cartesian, cylindrical or spherical. The coordinates in these are:

  • Cartesian (x,y,z)(x,y,z)
  • Cylindrical (r,θ,z)(r,\theta,z)
  • Spherical (r,θ,φ)(r,\theta,\varphi)

An axis is defined by three vectors irrespective of axis type. These define the location and basic orientation. The x\mathbf{x} axis vector is any vector pointing in the positive x\mathbf{x} axis direction. The xy\mathbf{xy} plane vector is any vector in the xy\mathbf{xy} plane of the axis that is not parallel with the x\mathbf{x} axis vector. The axes are then constructed as follows:

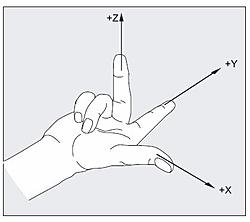
x=xaxis∣xaxis∣z=x×xyplane∣x×xyplane∣y=z×x\begin{aligned}\mathbf{x} &= \frac{\mathbf{x}_{axis}}{\left| \mathbf{x}_{axis} \right|} \\ \mathbf{z} &= \frac{\mathbf{x} \times \mathbf{x}\mathbf{y}_{plane}}{\left| \mathbf{x} \times \mathbf{x}\mathbf{y}_{plane} \right|} \\ \mathbf{y} &= \mathbf{z} \times \mathbf{x}\end{aligned}

The basic axis system is the Global Cartesian axis system, normally referred to as the Global axis system. All other axis systems are located relative to the Global axis system. Global axis directions are generally denoted X, Y and Z to distinguish from other, more general axis directions which use x, y and z.

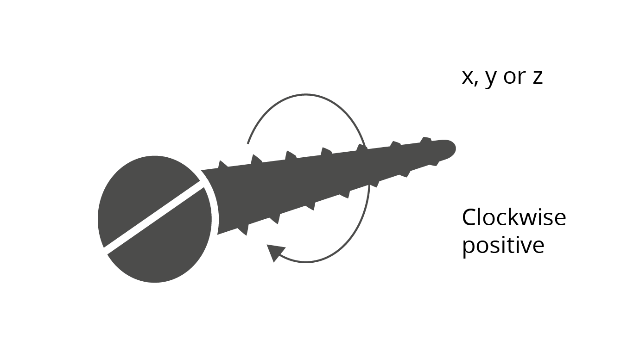
All the axes systems in GSA are right handed axes systems. Rotations about the axes follow the right hand screw rule