Spring Elements And Node Springs
Spring elements and node springs can one of several types.
The general spring has 6 degrees of freedom. For a linear spring the general form of the stiffness matrix is
If nonlinear spring are required these can be generated by assigning a material curve (force/displacement or moment rotation) to each of the degrees of freedom.
Axial / torsional spring
For an axial or torsional spring only the or terms are specified, the rest are assumed to be zero.
Spring matrix
For a node spring a full set of stiffness terms can be defined for the upper triangle. This allows interaction between axial and bending terms. The stiffness matrix is then of the form
A spring matrix can only be used with a node spring.
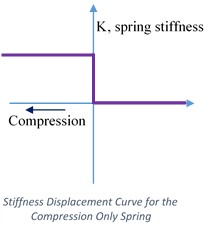
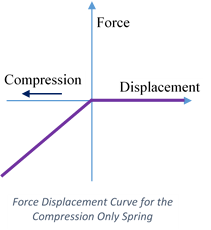
Compression-only spring
Compression only spring elements are uniaxial nonlinear spring elements. These elements have no stiffness when subjected tensile loading/displacements. Under tensile loading these elements will create a gap.
 |  |
|---|
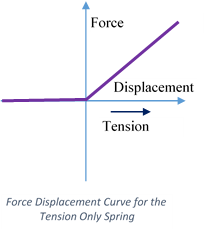
Tension-only spring
Tension only spring elements are also uniaxial nonlinear spring elements. These elements have no stiffness under compressive loading.
 |  |
|---|
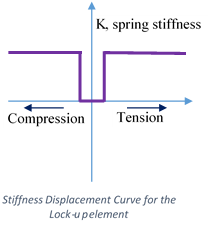
Lock-up
Lock-up elements are also uniaxial spring elements with specified initial gaps. Lock-up elements can be visualized as the combination of compression only and tension only spring with initial gaps. These spring elements do not offer any stiffness while the displacements are within the specified gap. Positive Gap will offer no resistance in the tension side and vice versa. Both positive and negative gaps have to be specified as positive values in GSA.
 | 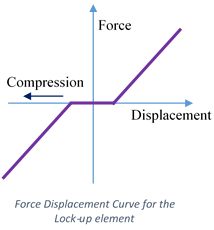 |
|---|
Connector
Connector elements are linear elastic spring elements. These elements connects pair of nodes in all translations as well as rotations. The size of the stiffness matrix is 12x12 and the same will be automatically calculated based on the stiffness of the surrounding elements. The resulting stiffness is large enough to produce negligible displacements and at the same time it will avoid the numerical instabilities.
Gap elements
Gap elements are compression only spring elements with initial gap. These elements will have zero stiffness in the analysis while the displacements are within the specified gap. The stiffness in other directions (local y and z directions) are ignored. These elements are useful in contact problems if frictional sliding is not concern.
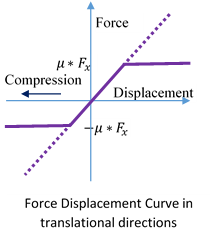
Friction elements
Friction elements are three direction translational spring elements consisting of one axial and two translational directions. In axial direction, these elements works as Gap elements. In translational direction these elements behaves as elastic plastic elements. Plastic limit is calculated using coulomb friction law
Where is the force in axial direction as calculated for the gap element.
 |  |
|---|
Springs are assumed to be massless.