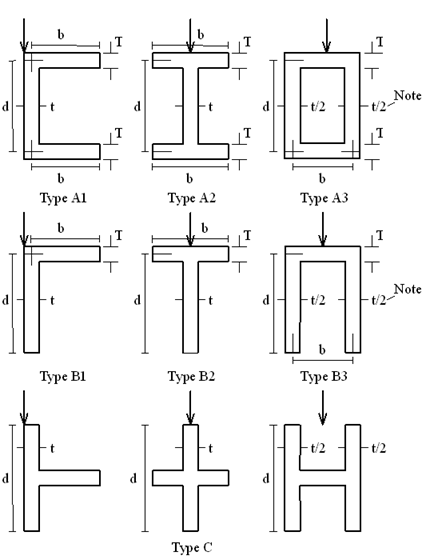
Thin Walled Sections
The effect of shear deformation on the results of a structural analysis is usually negligible. Where it is more significant, it will usually suffice to make a simple approximation to the shear deformation area of members with a cross-section such as those shown in Fig 1. The usual approximation is, by analogy with a simple rectangular beam, to take or of the total web area (overall depth × web thickness).
For those rare structures where the shear deformation is very important it may be necessary to use a more exact value for the area. This Note gives formulae for for the cross-sections of Fig.1 where
These were derived from the virtual work formula, shear deflection per unit length = . Here is the shear flow at any point at the middle of the wall thickness, the shear stress is assumed constant across the wall thickness , and the integration extends over the whole cross-section.
To see what the formulae mean in practice, they were applied to steel sections taken from the handbook with the results shown in the table below. In a web or flange with varying thickness, was assumed constant at its average value. The smaller values of in a range correspond to cross-sections with squarer aspect ratios. Samples only of UBs, UCs and channels were taken.
It can be seen that, for sections with top and bottom flanges bending, as nature intended, in their strong direction, the usual approximation is satisfactory (although it should be noted that d is the distance between flange centres, not overall depth). For the more bizarre sections used in bending, values of are seen to be lower than expected, especially when they are perversely bent in their weakest direction.
| Section | F |
|---|---|
| Bending in strong direction | |
| UB | 5.72 to 5.81 |
| Joist | 5.17 to 5.78 |
| UBP | 5.25 to 5.28 |
| UC | 5.28 to 5.53 |
| SHS | 5.0 |
| RHS | 5.0 to 5.49 |
| Channel | 5.06 to 5.60 |
| Angle | 3.68 to 4.62 |
| Tee from UB | 4.78 to 4.97 |
| Tee from UC | 4.11 to 4.35 |
| Cruciform | 5 |
| Bending in weak direction | |
| Channel | 2.12 to 3.78 |
| RHS | 4.02 to 5.0 ) |
| Angle | 2.55 to 3.68 (for = 0.5 to 1) |
| I’s, T’s, & cruciform | 5.0 |
With regard to calculating shear stresses, the exact distribution is not normally required, or even usable, because Codes of Practice base the shear strength on an allowable average shear stress calculated on the total net area . However, the shear distribution is sometimes required to design welds or concrete stitches, and, since it was found in the process of deriving the formulae for , formulae for the stress factors and are given. Here,
is the shear flow in the web at the junction with the flange, and
is the maximum shear flow in the web, in which is the shear force at the section.
For circular annuli, assuming that the stress is constant across the wall thickness , both the deflection and maximum stress can be obtained using a shear area of half the actual area, that is where is the mean radius.
Formulae
Shear deformation area
Type A1
Types A2 & A3
Special case of A3 with constant wall thickness so that
Type B1
Special case of B1 with constant
Types B2 & B3
Special case of B3 with constant thickness
Type C
Stress Factors
Type A1, A2 & A3
Type B1, B2 & B3