Updated Element Axes
In a geometrically nonlinear analysis the axes of the element must deform with the element. This has to resolve the difference between the original (undeformed) configuration and the current (deformed) configuration.
For 1D elements the deformed direction cosines can be represented by a new x vector based on the deformed positions of the ends of the element and the average rotation of the element about its x-axis.
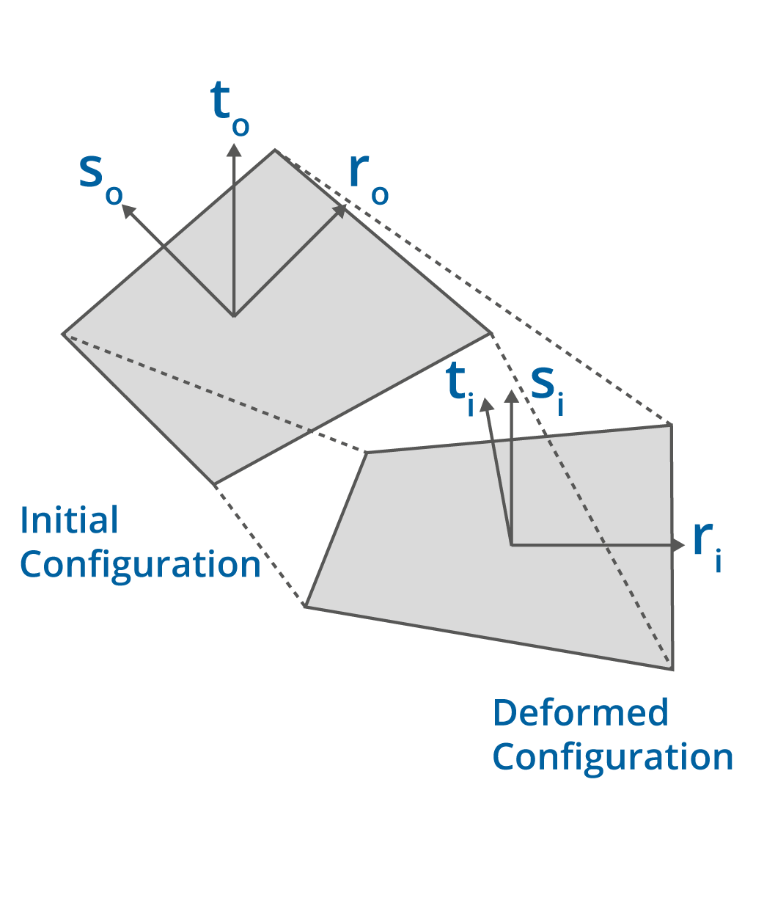
For 2D elements the undeformed configuration can be represented by direction cosines based on the axes.
The deformed configuration at can be represented by direction cosines based on the deformed axes.
The base direction cosines can then be updated using